
Another famous name in mathematics is the Pythagoras theorem. Named after the ancient Greek mathematician Pythagoras, it has always been a crucial idea in geometry and is used extensively in problem-solving, construction, architecture, and today, in hi-tech applications. This blog will discuss the Pythagoras theorem formula, proof, examples, and give a simplified version of the Pythagorean theorem for students.
What Is the Pythagoras Theorem?
Definition:
Pythagoras theorem, in a right-angled triangle, states that the square of the hypotenuse (side opposite the right angle) is equal to the sum of the squares of the other two sides.
This property can be expressed in its very simple formula.
Pythagoras Theorem Formula
If a right triangle has:
Base = a
Perpendicular (height) = b
Hypotenuse = c (longest side)
Then the formula reads as:
a² + b² = c²
Pythagoras Theorem
Imagine that you make squares on each of the three sides of a right triangle: the two smaller squares (on a and b) together will have an area equal to the larger square on c.
If one side were 3 units and the other 4, then:
a² + b² = 3² + 4² = 9 + 16 = 25
The hypotenuse c = √25 = 5
Therefore, a 3-4-5 triangle is an ideal right triangle.
Proving the Pythagorean Theorem
There are countless proofs of this theorem—algebraic proofs, geometric proofs, and visual proofs. Here is a very simple proof from the geometric side:
Draw a square with a side length of (a + b).
Next, situate within this square four copies of the right triangle with legs a and b and hypotenuse c.
The empty area in the middle will be a small square with a side c.
Now find the area of the big square in two different ways:
From the formula: Area = (a + b)²;
From the parts: Area = 4 × (½ab) + c² = 2ab + c².
Expanding the first expression yields: (a + b)² = a² + 2ab + b².
Set them equal: a² + 2ab + b² = 2ab + c².
Cancel the 2ab terms: a² + b² = c².
Steps to prove Pythagoras theorem explained in a clear cut manner.
Pythagoras Theorem Examples
Let us apply the formula to a few problems.
Example 1:
A ladder leans against a wall. The foot of the ladder is 9 m away from the wall, while the ladder reaches up to 12 m high. Find the length of the ladder.
a = 9, b = 12
c² = a² + b² = 9² + 12² = 81 + 144 = 225
c = √225 = 15 m
So, the ladder is 15 meters long.
Example 2:
Hypotenuse of a right triangle is 13 cm with one side as 5 cm. Find the other side.
c = 13, a = 5, b = ?
b² = c² - a² = 13² - 5² = 169 - 25 = 144
b = √144 = 12 cm
So, the missing side is 12 cm.
Example 3:
Verify if the triangle with side measurements 7 cm, 24 cm, and 25 cm is right-angled in nature.
a = 7, b = 24, c = 25
a² + b² = 49 + 576 = 625
c² = 25² = 625
Hence, this triangle is a right triangle.
Some Applications of Pythagoras Theorem
This theorem is not only theory in a book but comes with several applications:
Construction and Architecture → To make sure the walls are perfectly perpendicular.
Navigation → To find shortest paths (air, land, or sea).
Engineering → In the design of structures and machinery.
Computer Graphics → Distance calculations in 2D and 3D environments.
In everyday activities → Measuring diagonal distances, height of poles, and ladders leaning against walls.
Fun Fact about Pythagorean Triples
Numbers that satisfy the given theorem are called Pythagorean Triples. Probably the most famous of these are:
(3,4,5)
(5,12,13)
(7,24,25)
(8,15,17)
These triples are massively used for quick solving of geometry problems.
Conclusion
The Pythagoras theorem formula proof examples showcase that for any right-angled triangle, a² + b² = c².
Pythagorean theorem explained simply means the square of the hypotenuse is equal to the sum of the squares on the other two sides.
With everyday applications and plenty of examples, it remains one of the most useful theorems in mathematics.
Learning Pythagoras Theorem will help students in exams and further develop their ability to reason logically and visualize spatially.
Alpha Math offers a game-based learning experience with a unique four-step approach to mastering every concept in math. Schedule a Free Class Now
Article Author

Zarghoona Abid Khan is an experienced and passionate English instructor at Bambinos.live. She is dedicated to empowering students through effective teaching methodologies. Zarghoona is a graduate in English literature and a certified TEYL instructor. She possesses the knowledge and expertise to foster an engaging learning environment. Zarghoona efficiently teaches reading, writing, and English as a second language. She fosters a stimulating and inclusive learning environment and implements innovative approaches to enhance student engagement. Additionally, she utilizes various teaching resources and technologies effectively.
Latest Posts

No vs Not: Clear Grammar Rules, Usage, and Examples
Sep 29, 2025 5 min read
Types of Declarative Sentences: Definition, Uses & Examples
Sep 29, 2025 5 min read
Definition | What are Supplementary Angles?
Sep 29, 2025 5 min read
What Is Euphemism? – Meaning and Definition
Sep 29, 2025 5 min readSimilar Posts

The do’s and dont’s during your childs early education
May 15, 2020 5 min read
Why do you need to focus on child fitness?
May 16, 2020 5 min read
How parents can help boost their child’s personality development?
May 28, 2020 5 min read
How can personality development classes benefit teenagers?
Jun 05, 2020 5 min read
Multiple Intelligences - Explore and Discover the Learning Style of Your Child
Aug 21, 2020 5 min read
5 Benefits of Bambinos Phonics Course For 4–7-Year-Old
Jan 13, 2024 5 min read
10 Good habits and values every parent must teach their child
Jan 24, 2024 5 min read
30 Positive Thoughts for the Day to Inspire your Kids to go to School
Jan 24, 2024 5 min read
Best books for english speaking | Learn English | Improve English
Jan 25, 2024 5 min read
10 Tips to improve public speaking skills in children
Feb 08, 2024 5 min read
20 Short Moral Stories for kids in English | Valuable Lessons
Feb 10, 2024 5 min read
Listen Your Way to English Proficiency: Mastering the Art of Listening
Feb 13, 2024 5 min read
10 Must Read Classics For Your Child
Feb 13, 2024 5 min read
Best TV shows that you can watch along with your child
Feb 14, 2024 5 min read
7 Best Extracurricular Activities for your Children
Feb 17, 2024 5 min read
How To Help A Child With Exam Stress | A Parents Guide
Feb 17, 2024 5 min read
10 Personality Development Tips for Kids
Feb 17, 2024 5 min read
CBSE vs ICSE vs IB - What are the differences and which is the best choice for your child
Feb 22, 2024 5 min read
7 Ways Teach Self-Discipline Skills to kids
Feb 22, 2024 5 min read
Top 10 schools for children in Delhi/NCR
Feb 23, 2024 5 min read
Breaking Down Barriers: The Importance of English as a Global Language
Feb 23, 2024 5 min read
10 Influencers Making a Difference With Their Parenting Tips
Feb 24, 2024 5 min read
5 Ways to Deal with a Stubborn Kid
Feb 27, 2024 5 min read
Adventure Learning: Fun STEM based activities for children
Feb 28, 2024 5 min read
Prevent Your Child’s Mobile Addiction
Feb 28, 2024 5 min read
What Difference a Father Makes: Importance of Equal Parenting
Feb 29, 2024 5 min read
Colourful Holi Activities for Kids
Mar 05, 2024 5 min read
Develop Positive Habits: Build a Healthy Lifestyle for Your Kids
Mar 05, 2024 5 min read
Easy Ways to Teach Consonant Blends, Digraphs and Trigraphs
Mar 14, 2024 5 min read
Homeschooling Tips For Working Parents
Mar 15, 2024 5 min read
Making Verbs Easy for kids: Exploring the Action Words
Mar 16, 2024 5 min read
Educational Pathways in India: Traditional, Homeschooling, and Unschooling
Mar 28, 2024 5 min read
Opinion Writing Made Easy: Engaging Strategies for Elementary Students
Mar 28, 2024 5 min read
Mothers Day Speech
Mar 29, 2024 5 min read
Impact of the Reducing Green Cover of Earth
Apr 01, 2024 5 min read
With AI Taking Over Technology Learning English Remains a Key step
Apr 02, 2024 5 min read
Why is Bambinos the perfect public speaking learning platform for your kid
Apr 09, 2024 5 min read
Top 15 Spoken English Books to Enhance Your Fluency
Apr 17, 2024 5 min read
100+ Public Speaking Topics and Ideas
Apr 18, 2024 5 min read
15 Phonics Rules For Reading and Spelling Success
Apr 19, 2024 5 min read
Role of Parents in Child's Development
Apr 19, 2024 5 min read
Top 110+ Easy English Speech Topics for Students
Apr 25, 2024 5 min read
AI in Education: The Advantages and Disadvantages
Apr 25, 2024 5 min read
Farewell Speech for Colleague
Apr 29, 2024 5 min read
How to Write Alphabets in Cursive: Step-by-step Guide for Kids
May 24, 2024 5 min read
Best Inspirational Quotes About Parenthood
May 28, 2024 5 min read
How to Improve Handwriting: 10 Effective Tips for Parents
May 28, 2024 5 min read
30 Best Thank You Note for Teachers
May 28, 2024 5 min read
10 Free Online Classic Storybooks for Kids
May 29, 2024 5 min read
25 Powerful Education Quotes for Kids
May 29, 2024 5 min read
50 Interesting Debate Topics for Kids of All Ages & Grades
May 30, 2024 5 min read
How to Be a Good Debater - Complete Guide to Debating
Jun 27, 2024 5 min read
Living Things & Non-Living Things – Definition, Examples, And Characteristics
Jul 03, 2024 5 min read
Best Online Coding Classes for Kids
Jul 11, 2024 5 min read
Acing Fluency - How to Speak in English on Any Topic Effortlessly
Jul 12, 2024 5 min read
List of Best Companies Teaching Kids English Phonics Skills in India
Jul 13, 2024 5 min read
Overcoming Stage Fright: Tips and Tricks for Confident Public Speaking
Jul 16, 2024 5 min read
Fantastic Novels to Enhance English from Beginner to Advanced
Jul 21, 2024 5 min read
Descriptive Words: Everyday words for Kids to learn
Jul 23, 2024 5 min read
Essay On Earth – 10 Lines, Short And Long Essay For Kids
Jul 27, 2024 5 min read
Why is Body Language Important in Communication Skills?
Jul 28, 2024 5 min read
Phonics vs. Whole Language – Which is Best for Your Child?
Aug 06, 2024 5 min read
Common Mistakes Parents Make When Teaching Spoken English to Kids
Aug 07, 2024 5 min read
How to Encourage Your Child to Write from the Heart
Aug 08, 2024 5 min read
How to Create an English-Speaking Environment at Home
Aug 13, 2024 5 min read
The Connection Between Public Speaking and Leadership Skills in Kids
Aug 15, 2024 5 min read
The Connection between Math and Real-Life Problem-Solving
Aug 18, 2024 5 min read
How to make writing fun for your children
Aug 25, 2024 5 min read
10 Key Benefits of Phonics Instruction for Young Readers
Aug 28, 2024 5 min read
How to Choose the Right Phonics Program for Your Child
Aug 28, 2024 5 min read
15 Fun Social Emotional Activities for Preschool & Kindergarten
Sep 05, 2024 5 min read
15 Best Funny Math Memes for Kids: Adding Humor to Math
Sep 06, 2024 5 min read
How to Teach Long Division to Kids in 6 Easy Steps
Sep 16, 2024 5 min read
How to Teach Division to Kids in 11 Easy Steps
Sep 18, 2024 5 min read
8 Math Division Tricks: Making Division Fun & Accessible
Sep 19, 2024 5 min read
How to Encourage Your Child to Write with Imagination
Sep 21, 2024 5 min read
30 Best Multiplication Tricks to Solve Complex Math Problems
Sep 23, 2024 5 min read
10 Best Boarding Schools in the USA
Sep 30, 2024 5 min read
How to Teach Number Recognition to Kids in 10 Easy Steps
Oct 21, 2024 5 min read
Simple & Stress-Free After School: Schedule for Kids of All Ages
Oct 29, 2024 5 min read
Water Pollution Essay: Causes, Effects and Solutions
Nov 06, 2024 5 min read
Mastering Dialogue Writing in English: Tips and Techniques
Nov 07, 2024 5 min read
Learn with a Phonics Sound Chart: Pronunciation Guide for Young Learners
Nov 12, 2024 5 min read
How to Overcome Public Speaking Fear in Children
Nov 13, 2024 5 min read
Fruits Name in English: Fun Examples for Kids to Learn!
Nov 18, 2024 5 min read
Makar Sankranti Essay: Celebrating the Festival of Harvest
Nov 18, 2024 5 min read
Acknowledgment for Assignment: Format, Samples, and Tips!
Nov 25, 2024 5 min read
Learn English for Kids with Bambinos - A Comprehensive Approach
Nov 27, 2024 5 min read
How to Choose Age-Appropriate Books for Young Readers
Dec 07, 2024 5 min read
10 Fun Ways For Parents to Boost their Kids Vocabulary At Home
Dec 09, 2024 5 min read
The Role of Public Speaking Classes in Enhancing Spoken English Skills
Dec 10, 2024 5 min read
The Role of Phonics in Building a Robust Vocabulary for Young Learners
Dec 13, 2024 5 min read
Akaay (Virushka's son) Meaning: Connection to Hinduism
Dec 14, 2024 5 min read
How Math Classes at Bambinos.live Turn Numbers into Fun
Dec 17, 2024 5 min read
Breaking Down Big Numbers: How to Tackle Complex Math Problems with Confidence
Dec 20, 2024 5 min read
How Phonics Classes at Bambinos.live Make Learning Fun for Kids
Dec 24, 2024 5 min read
Why Phonics is the Foundation of Reading and Writing Success
Dec 25, 2024 5 min read
From ABCs to Reading Fluency: The Step-by-Step Journey with Phonics
Dec 25, 2024 5 min read
Bambinos.Live: From Start-Up to Shark Tank Success
Dec 25, 2024 5 min read
Phonics Classes Online vs Offline: Which is Right for Your Child?
Dec 27, 2024 5 min read
How Bambinos.live is Transforming Online Education for Children
Dec 27, 2024 5 min read
Success Stories: How Bambinos.live is Enhancing Children's English Skills
Dec 30, 2024 5 min read
Why Phonics is the Key to Your Child’s Reading Success?
Dec 30, 2024 5 min read
Behind the Scenes: The Founders' Journey of Bambinos.live
Dec 31, 2024 5 min read
The spiritual and Ethical Benefits of Bhagavad Gita Lessons for kids
Dec 31, 2024 5 min read
Top 10 English Learning Platforms for Kids in 2025
Jan 02, 2025 5 min read
Why Bhagavad Gita lessons are ideal for children aged 4-15 years
Jan 08, 2025 5 min read
The Relevance of Bhagavad Gita in today's time and age: Lessons for Kids
Jan 09, 2025 5 min read
Summer Vacation Essay for Students in English: Memorable Experiences
Jan 09, 2025 5 min read
Planet Spark or Physics Wallah vs Bambinos.live: Which Offers the Best Value
Jan 10, 2025 5 min read
What Do Parents Say? Planet Spark Reviews vs Bambinos.live Reviews
Jan 11, 2025 5 min read
Bhanzu vs Bambinos.live: Comparing Features, Costs, and Parental Feedback
Jan 11, 2025 5 min read
Where to Find Public Speaking Classes for Kids in Bangladesh
Jan 11, 2025 5 min read
Exploring the National Festivals of India: An Informative Essay
Jan 14, 2025 5 min read
How Many Days in 72 Hours? – Simple Time Conversion Guide
Jan 15, 2025 5 min read
The Importance of Early Math Skills: A Guide for Parents
Jan 15, 2025 5 min read
Understanding Amavasya and Its Importance
Jan 21, 2025 5 min read
The Best Online Math Classes for Kids in Bangladesh
Jan 24, 2025 5 min read
IQ Test for 10 & 12-Year-Olds: Basics, Questions, Scores
Jan 27, 2025 5 min read
How to Convert 40 cm to Inches: The Definitive Guide
Jan 30, 2025 5 min read
How Many Seconds in a Day
Jan 30, 2025 5 min read
Mathematics classes in Bangladesh: online and offline Options for students.
Feb 06, 2025 5 min read
10 Daily Routine for Students Going to School
Feb 08, 2025 5 min read
How to convert units of Length, Area and Volume
Feb 12, 2025 5 min read
Why Algebra Matters: Understanding Why is Algebra Important in Everyday Life?
Feb 12, 2025 5 min read
50 GK Questions for Class 2
Feb 19, 2025 5 min read
50 GK Questions for Class 6 kids
Feb 19, 2025 5 min read
Importance of having Good Habits for Kids
Feb 19, 2025 5 min read
How to Teach Subtraction to Kids: 10 Best Methods
Feb 24, 2025 5 min read
Which 10 schools are best in Hyderabad
Feb 28, 2025 5 min read
The Importance of Parents in Life - Roles and Actions
Feb 28, 2025 5 min read
Applications of Fractions in Daily Life: Real World Applications in Life
Feb 28, 2025 5 min read
What is Gayatri Mantra Meaning, Benefits and Rules
Feb 28, 2025 5 min read
Root Words, Suffixes, and Prefixes
Mar 15, 2025 5 min read
Pre-Number Concept for Beginners
Mar 19, 2025 5 min read
50 GK Questions for Class 4
Mar 20, 2025 5 min read
30 Fun Math Questions with Answers
Mar 25, 2025 5 min read
50 GK Questions for Class 8
Mar 27, 2025 5 min read
50 GK Questions for Class 3
Mar 29, 2025 5 min read
20 kg to lbs conversion: How many pounds is 20 kg
Apr 02, 2025 5 min read
Speed, Acceleration, and Time | m/s to km/h, etc. | Examples
Apr 02, 2025 5 min read
Abacus: A brief history from Babylon to Japan
Apr 02, 2025 5 min read
Notice Writing: Format, Samples, and Writing Tips
Apr 12, 2025 5 min read
How to Solve Math Word Problems: 10 Effective Strategies
Apr 16, 2025 5 min read
200 Celsius to Fahrenheit: How to Convert 200 C to F
Apr 19, 2025 5 min read
15CM to Inches Conversion: How Many Inches are 15 CM?
Apr 24, 2025 5 min read
40 Celsius to Fahrenheit, 40°C to °F Conversion
Apr 24, 2025 5 min read
Akshaya Tritiya 2025: Whom is Blessed On This Auspicious Day? Gods & Rituals
Apr 25, 2025 5 min read
Time management skills and techniques for students
Apr 26, 2025 5 min read
Informal Letter: Format, Samples, and Writing Tips
Apr 29, 2025 5 min read
The Basic Spelling Vocabulary List for kids in grades 1–5
Apr 29, 2025 5 min read
Teaching Basic Shapes to Kids In an Interesting Way
Apr 30, 2025 5 min read
What Should be Included in the Preschool Curriculum? A Detailed Guide
Apr 30, 2025 5 min read
Feet to CM (ft to cm) Conversion – Formula, Height Chart, Examples
May 13, 2025 5 min read
English Grammar Nouns for Class 3
May 14, 2025 5 min read
English Grammar Nouns for Class 1
May 15, 2025 5 min read
English Grammar: Noun for Class 4 – A Simple Guide
May 15, 2025 5 min read
Thousand (1,000) in Math – Definition, Facts, Examples, FAQs
May 16, 2025 5 min read
Kilometers to Miles Conversion (km to mi): Formula, Steps, Examples
May 16, 2025 5 min read
What are Nouns?
May 26, 2025 5 min read
English Grammar - Articles for Class 6
May 26, 2025 5 min read
What is Zero – Definition with Examples
May 29, 2025 5 min read
Even Numbers and Odd Numbers – Properties, Examples
May 29, 2025 5 min read
English Grammar Adjective for Class 4
Jun 14, 2025 5 min read
Can vs. May: How to Use Them – A Quick English Lesson
Jun 18, 2025 5 min read
How Lakshmi Teaches Us Discipline, Gratitude, and Abundance
Jun 18, 2025 5 min read
What are Consonant Blends and Why are They Important?
Jun 26, 2025 5 min read
English Grammar Adjective for Class 1
Jun 26, 2025 5 min read
What is Quarter Past? Definition, Examples, Facts
Jun 26, 2025 5 min read
Sector of a Circle: Definition, Formula, Area, Perimeter, Examples
Jun 26, 2025 5 min read
What is Quarter in Math? Definition, Fraction, Examples, Facts
Jun 26, 2025 5 min read
English Grammar Adjective for Class 2
Jun 26, 2025 5 min read
The Differences Between British English and American English
Jun 27, 2025 5 min read
What is Distributive Property? Definition, Formula, Examples
Jun 27, 2025 5 min read
Feet to Meters Conversion - Formula, Examples, Facts, FAQs
Jun 28, 2025 5 min read
What are Compound Words: Types, Examples & List
Jul 07, 2025 5 min read
English Grammar Adjective for Class 3
Jul 16, 2025 5 min read
What is Associative Property? Definition, Facts, and Examples
Jul 16, 2025 5 min read
Shakuntala Devi: A Human Computer
Jul 30, 2025 5 min read
Speech on Corruption for Kids
Jul 30, 2025 5 min read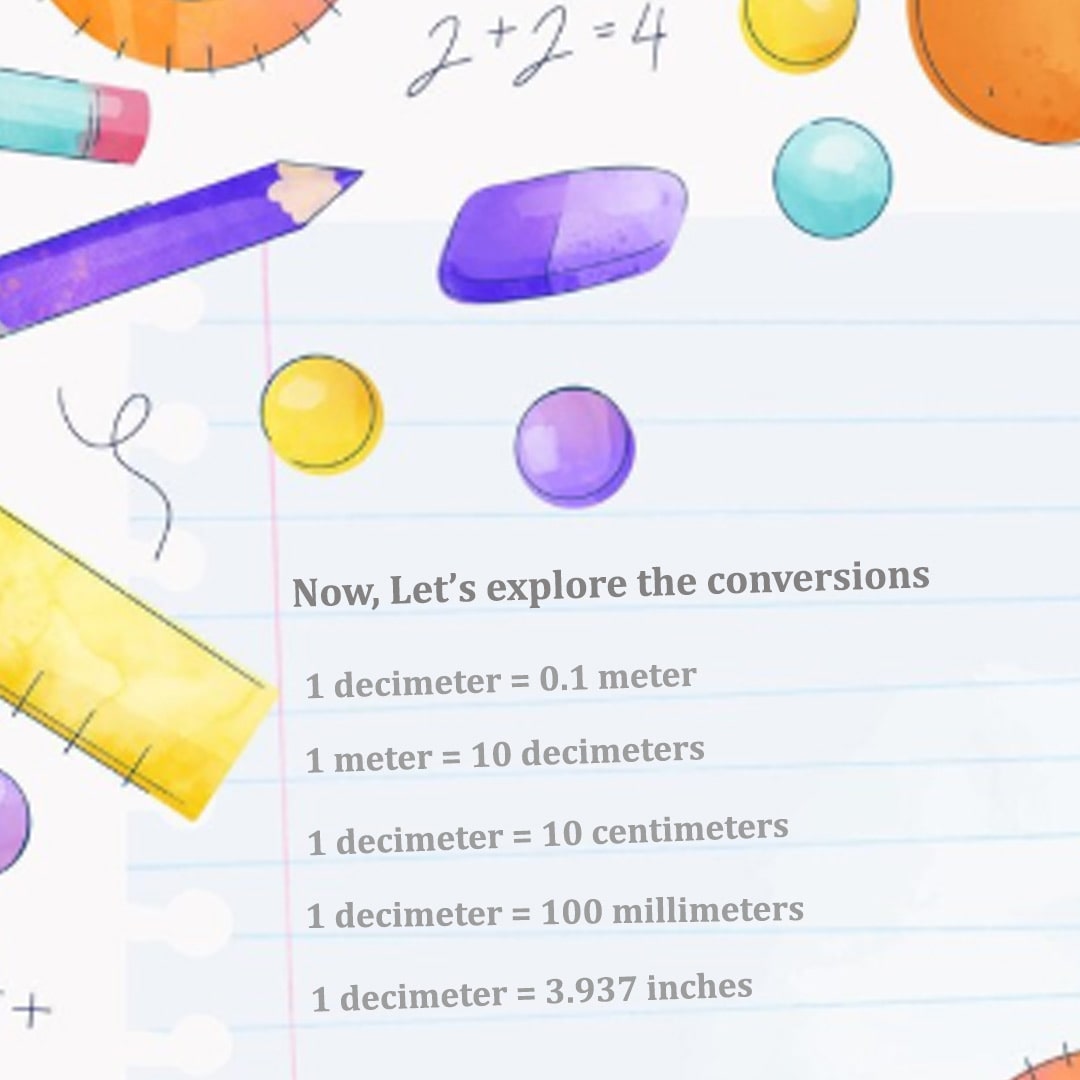
Decimeter: The Unit Facts and Examples
Jul 30, 2025 5 min read
Speech writing for kids: Tips to write fun, engaging speeches
Jul 31, 2025 5 min read
Speech on Discipline: Importance, Benefits and Sample Speeches for Students
Aug 01, 2025 5 min read
Hindu Symbols and Their Meanings for Children: A Magical Adventure of Ancient Knowledge
Aug 01, 2025 5 min read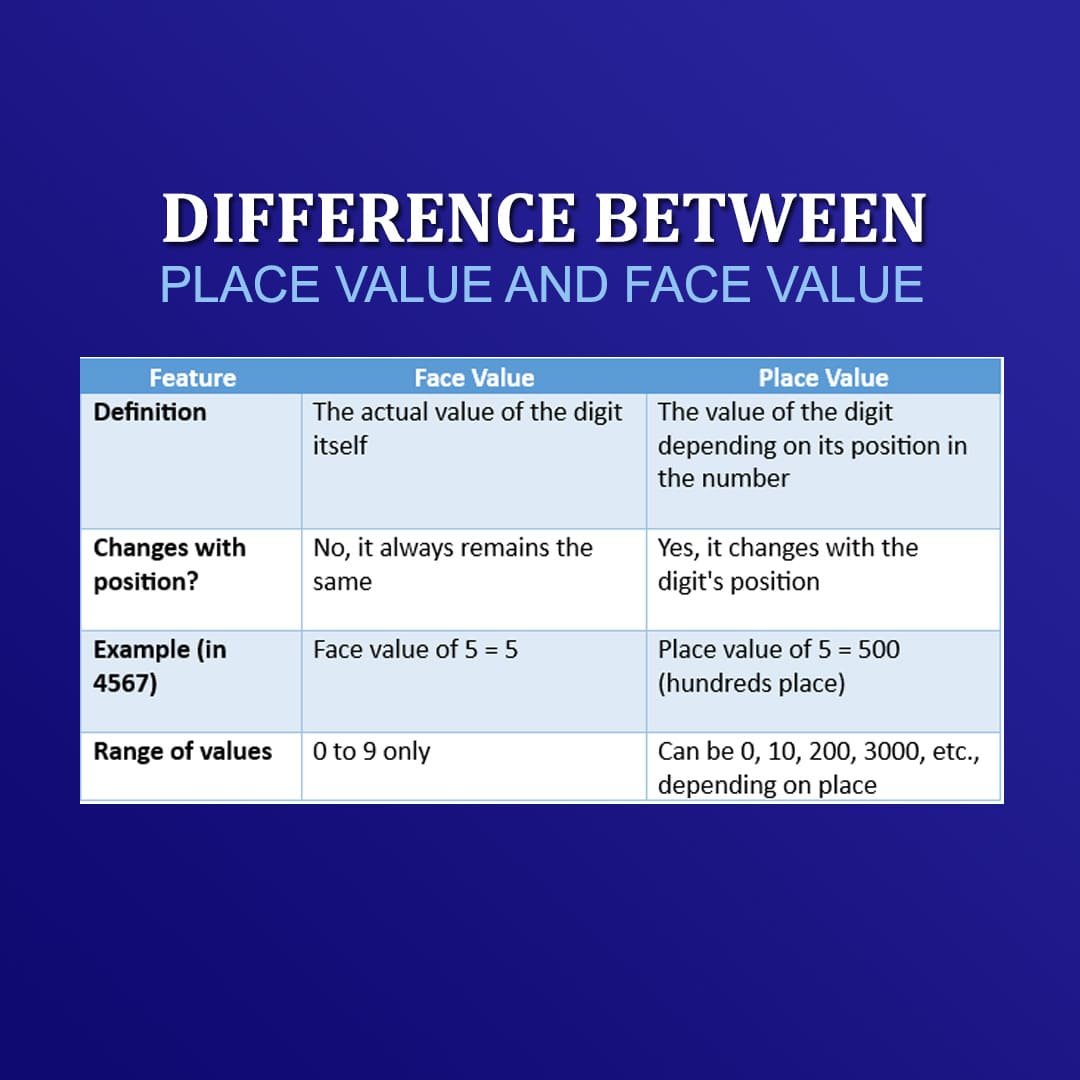
Difference Between Place Value and Face Value
Aug 27, 2025 5 min read
Funny Tongue Twisters for Tickling your Tongue
Aug 27, 2025 5 min read
Debate Writing Class 11 | Format, Samples & Skills
Aug 29, 2025 5 min read
What Is a Prefix and a Suffix? – Meaning and Definition
Aug 29, 2025 5 min read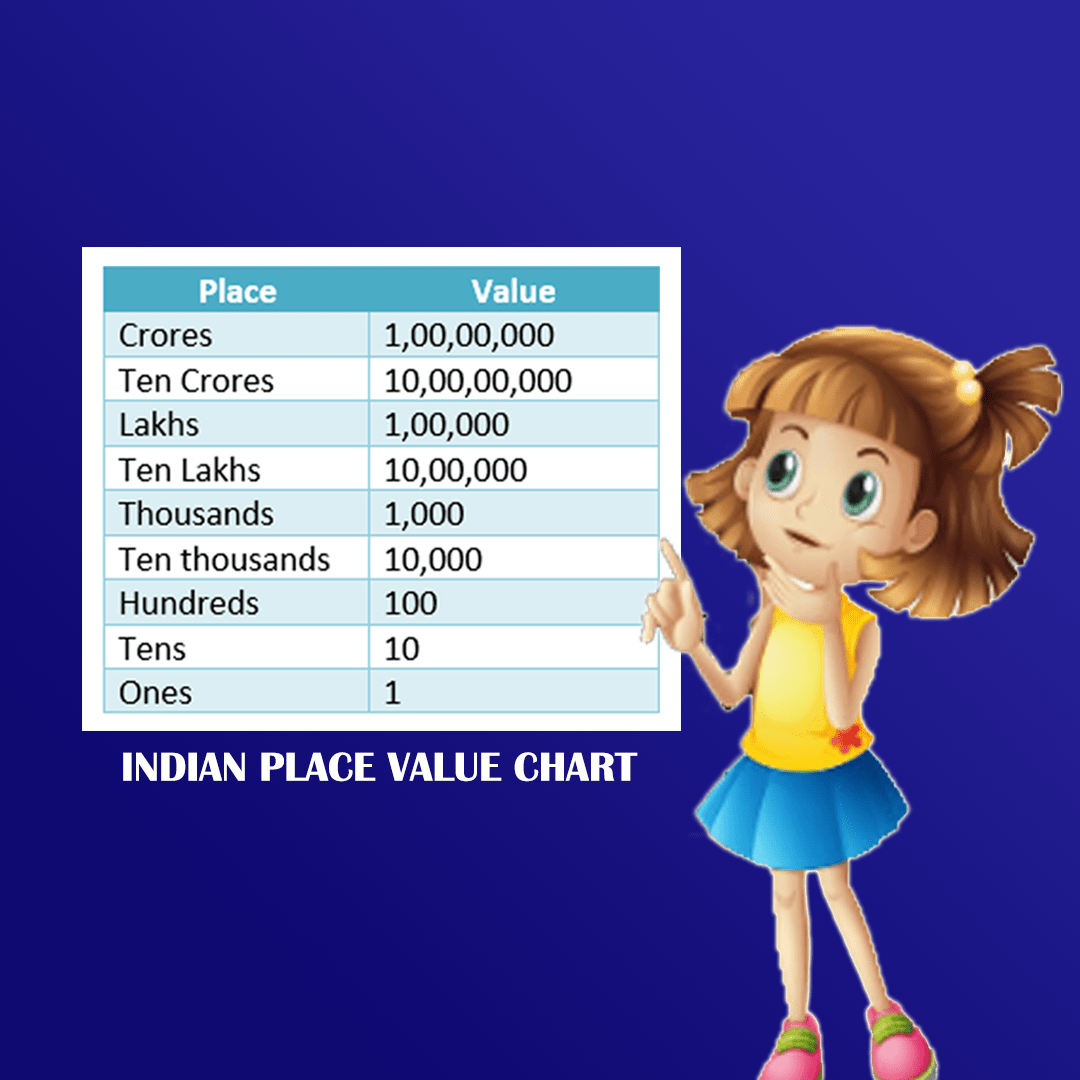
Indian Place Value Chart
Aug 29, 2025 5 min read
Definition, Examples | Rational and Irrational Numbers
Aug 29, 2025 5 min read
Prime numbers definition and example
Aug 29, 2025 5 min read
Relation Between Inch and Centimeter – Formula, Conversion, Examples
Aug 29, 2025 5 min read
Difference between Women and Woman
Aug 30, 2025 5 min read
What Is an Acronym? Definition and Examples
Aug 30, 2025 5 min read
Personification (Figure of Speech) – Meaning, Examples & Usage
Aug 30, 2025 5 min read
Bhagavad Gita Quotes for Kids on Karma: Simple Lessons for Children
Aug 30, 2025 5 min read
10 Best Bhagavad Gita Stories in English
Sep 01, 2025 5 min read
Numeral System: Indian And International
Sep 01, 2025 5 min read
Greater Than and Less Than Symbols Definition
Sep 01, 2025 5 min read
How to Teach Phonics to Kindergarten Kids (2025 Trends)
Sep 01, 2025 5 min read
What Is Oxymoron? – Meaning and Definition
Sep 29, 2025 5 min read
Parallelogram – Shape, Definition, Formulas, Properties, Examples
Sep 29, 2025 5 min read
What are Equivalent Fractions? Definition & Examples
Sep 29, 2025 5 min read
Coprime Numbers - Definition, Meaning, Examples
Sep 29, 2025 5 min read
Difference Between Pound and Kilogram Explained
Sep 29, 2025 5 min read
What Is Euphemism? – Meaning and Definition
Sep 29, 2025 5 min read
Definition | What are Supplementary Angles?
Sep 29, 2025 5 min read
Types of Declarative Sentences: Definition, Uses & Examples
Sep 29, 2025 5 min read